Galileo Galilei údajně tvrdil, že matematika je jazyk, kterým Bůh napsal svět. Ať už to
tak bylo nebo ne, důležitým pro nás zůstává, že matematiku označil jako jazyk. To se
někomu možná může zdát zvláštní, je to ovšem velice trefné.
Brát matematiku za soubor čísel je stejné jako brát češtinu za soubor jednotlivých slov
– ve své podstatě ne vyloženě špatné, ovšem velmi, velmi omezené. Když naučíte
člověka celý slovník a nevysvětlíte mu, jak postavit větu, bude stejně bezradný jako
člověk, který strojově vyřeší kvadratickou rovnici a neuvědomí si, že most nemůže
měřit -28,4 metry.
Z trochu jiné strany. Otec, který je strojní inženýr a v oboru se pohybuje celý život, říkal, že
si do teď vystačil s násobilkou, goniometrickými funkcemi a Pythagorovou větou. Z jeho
pohledu je veškerá pokročilá matematika zbytečností, která se uplatní jen na vysoké škole. Ve
vzácných případech i v zaměstnání. Tento názor mě překvapil a trochu mi boří představu o
důležitosti matematiky. Otec je někdo, ke komu vzhlížím a od mala byl mým vzorem. Přesto
mi matika přijde důležitější než jen pro studium na vysoké škole.
MŠ: Možná máte pravdu oba. Ať studujete jakýkoliv obor, v praxi použijete jen zlomek.
Při studiu ale nejde jen o znalosti, ale i o kultivaci myšlení.
Při potýkání s obtížnými pojmy a problémy si vytváříte ve svém mozku propojení, která v budoucnu můžete použít i v jiném kontextu.
A jde o to, jaké kvality ta propojení jsou a to je hlavně na vás, ale je to i na nás, vašich učitelích.
Rostoucí inteligence počítačových programů však neznamená, že si můžeme
dovolit, aby ji obsluhoval čím dál tím „hloupější“ uživatel. Je potřeba mít nadhled nad
tím, jaké nám byly dodány výsledky a mít představu o tom, co nám může nebo nemůže
vyjít.
Děkuji za možnost vyjádřit se ke svému pohledu na matematiku a doufám, že
se mi bude dařit učivo matematiky v dostatečném rozsahu zvládat.
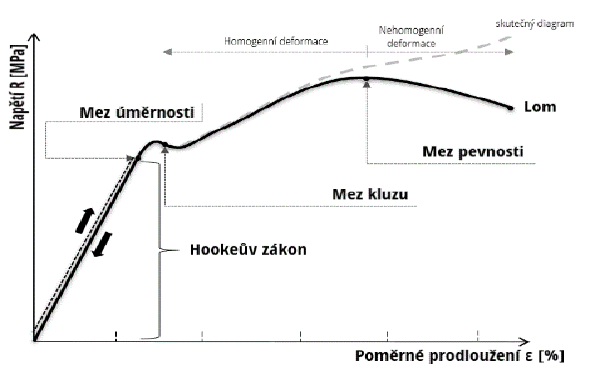
Kreslení funkcí v matematice je vlastně základ odečítání z grafů. Takže pokud
v nauce o materiálech se objevil třeba trhací diagram:
Tak si člověk, který má zkušenosti právě s funkcemi odvodil že hodnota (uvedu
příklad na obrázku) na ose x má vždy „parťáka“ v ose y.
Tedy „proměnné prodloužení má „parťáka“ v „napětí“ a když z těchto dvou hodnot
povedeme kolmici na ose x a na ose y vyjde nám průsečík těchto dvou kolmic a
v tomto bodě máme právě první bod té dané funkce. A když takhle uděláme
„nekonečně mnoho bodů“ vyjde nám krásný trhací diagram.
Studenti, kteří mají silný matematický základ, jsou
schopni rychleji identifikovat problémy a hledat efektivní řešení.
Jako studenti bychom měli rozumět problému a umět problémy i řešit, a ne
pouze zadávat hodnoty do programu, který z nich následně stanoví výsledek. Student jim musí
rozumět, aby je mohl zkontrolovat a pokud to bude potřeba, tak i předělat k lepšímu. Když se
například špatně navrhne nosník a spadne, tak vina nejde za strojem, ale za člověkem, který tu
danou věc měl na starost.
Teď po prvním měsíci na vysoké škole bych řekl, že už dokáži určit největší rozdíly ve výuce
matematiky v porovnání se střední školou. Zatímco na SŠ jsme vždy jen dostali zadání v podobě
jednoduché slovní úlohy nebo jenom jako samostatný příklad, tady se na problém (slovní úlohu)
musíme koukat komplexněji a znát už základní principy, které se k tomu vztahují.
Věřím, že matematika má co nabídnout a opravdu má cenu se jí
věnovat a nevystačit si akorát s minimem bodů pro úspěch v dané zkoušce či zápočtu.
