Přípravné opakovací kurzy
Přípravné opakovací kurzy 2025
Sylaby a skripta
Skripta pro přípravné kurzy jsou ke stažení zde:
Rozvrhy
Přípravné opakovací kurzy zejm. matematiky, fyziky a geometrie před nástupem do studia prvního ročníku v akademickém roce 2025/26. Rozvrhy
FM |
FS |
FT & FP (nově) |
|
|
|
|
|
Zahajovací schůzka
Každoročně organizujeme přípravné opakovací kurzy zejm. matematiky před nástupem do bakalářského studia prvního ročníku pro studenty vybraných fakult a studijních programů TUL. Zahajovací schůzka opakovacího kurzu proběhne v učebně:
- 🏢 Fakulta mechatroniky, informatiky a mezioborových studií v pondělí 1. 9. 2025 od 12:00 hodin v učebně E9.
- 🏬 Fakulta strojní v pondělí 1. 9. 2025 od 11:00 hodin v učebně C200.
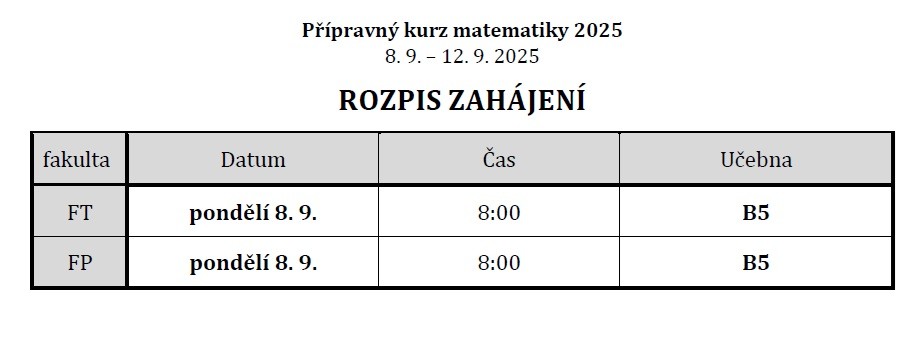
- 🏣 Fakulta textilní (spolu s FP) v pondělí 8. 9. 2025 od 8:00 hodin v učebně B5. (nově)
- 🏨 Fakulta přírodovědně-humanitní a pedagogická (spolu s FT) v pondělí 8. 9. 2025 od 8:00 hodin v učebně B5. (nově)
Pozvánka
Každoročně organizujeme přípravné opakovací kurzy zejm. matematiky před nástupem do bakalářského studia prvního ročníku pro studenty vybraných fakult a studijních programů TUL. Níže naleznete u názvu své fakulty případně porgramu pozvánka v PDF s detailními informacemi a odkaz na přihlašovací formulář.
Fakulta strojní
- ✉️ Pozvánka: zvaci_dopis_2025_FS.pdf
- 📋 Přihlašovací formulář: https://forms.gle/bCETw9E9wTTJFvew5
Fakulta mechatroniky, informatiky a mezioborových studií
- ✉️ Pozvánka: zvaci_dopis_2025_FM.pdf
- 📋 Přihlašovací formulář: https://forms.gle/jbNaJTf4FY9te53Y7
Fakulta přírodovědně-humanitní a pedagogická
program: Matematika se zaměřením na vzdělávání
- ✉️ Pozvánka: zvaci_dopis_2025_FP.pdf
- 📋 Přihlašovací formulář: https://forms.gle/v4P6uwQvarcXcTKX8
Přípravné opakovací kurzy 2024
Sylaby a skripta
Sylaby přípravných opakovacích kurzů matematiky, fyziky a geometrie:
- 📈 Matematika pro FM & FZS
- 📈 Matematika pro FT
- 📈 Matematika pro FS
- 📐 Geometrie pro FS
- 💡 Fyzika pro FS, FM & FZS
Skripta pro přípravné kurzy jsou ke stažení zde:
Rozvrhy
-
FT & FP
-
FS
-
FM & FZS
Zahajovací schůzka
Zahajovací schůzka přípravného opakovacího kurzu pro studující
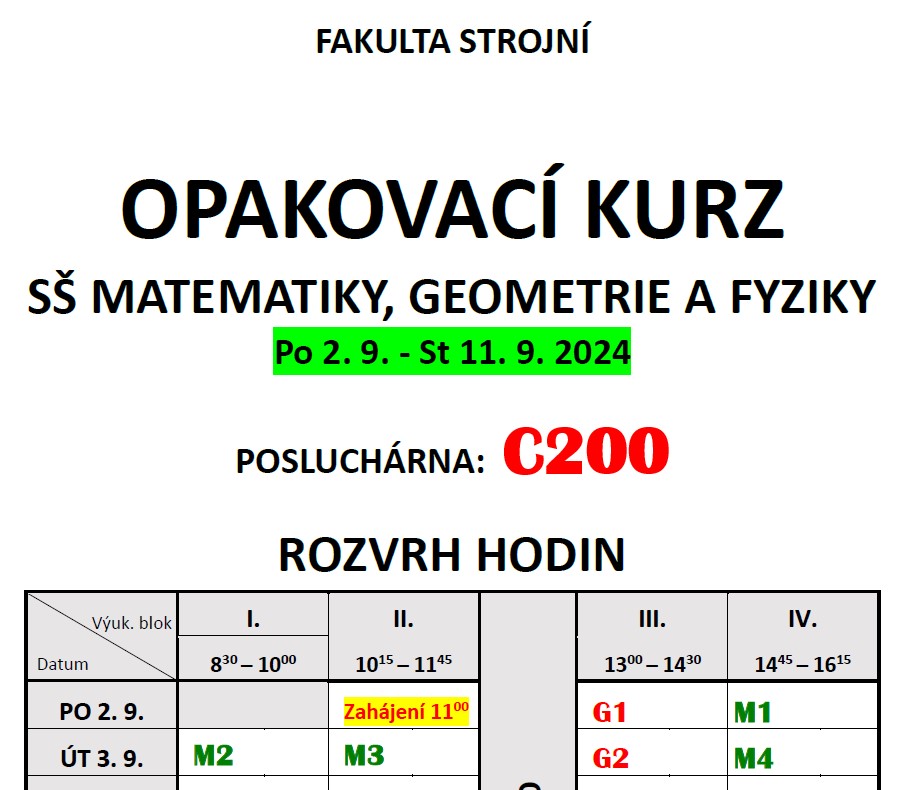
- 🏬 Fakulta strojní v pondělí 2. 9. 2024 od 11:00 hodin v učebně C200.
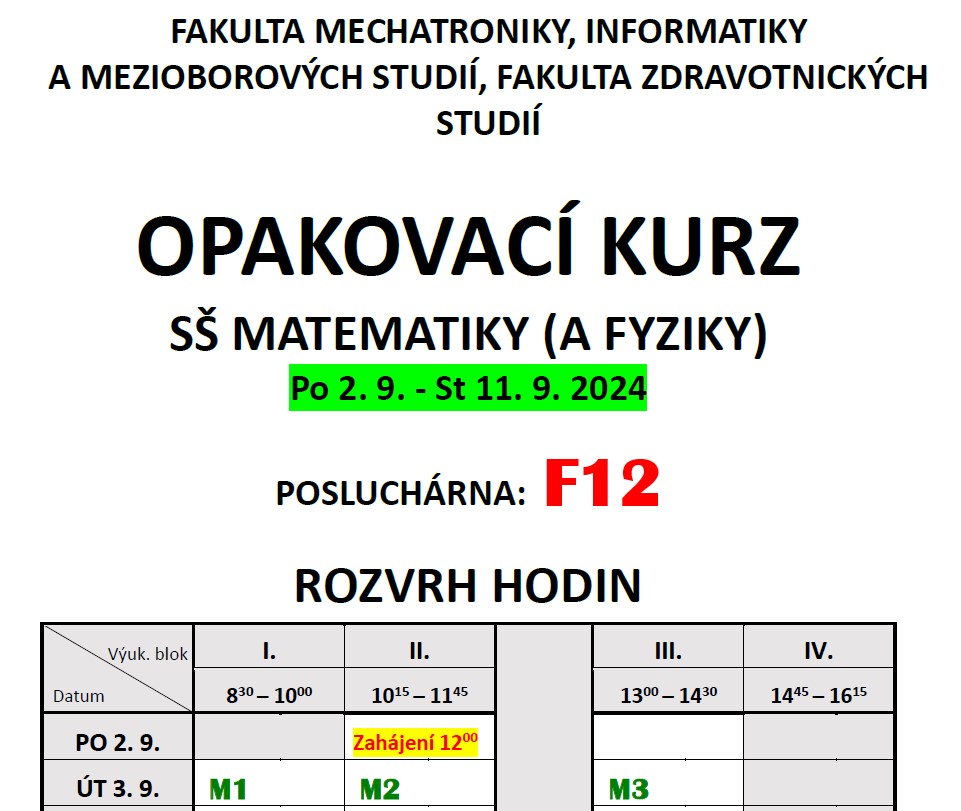
- 🏢 Fakulta mechatroniky, informatiky a mezioborových studií (spolu s FZS) v pondělí 2. 9. 2024 od 12:00 hodin v učebně F12 (budova menzy).
- 🏥 Fakulta zdravotnických studií (spolu s FM) v pondělí 2. 9. 2024 od 12:00 hodin v učebně F12 (budova menzy).
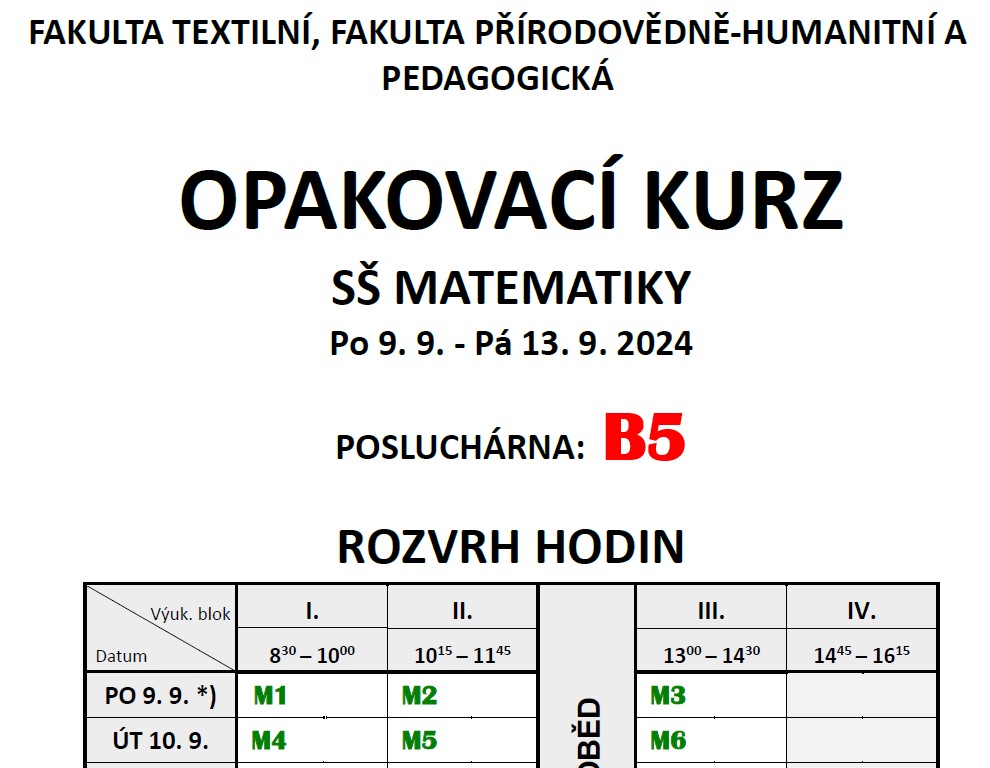
- 🏨 Fakulta přírodovědně-humanitní a pedagogická (spolu s FT) v pondělí 9. 9. 2024 od 8:00 hodin v učebně B5.
- 🏣 Fakulta textilní (spolu s FP) v pondělí 9. 9. 2024 od 8:00 hodin v učebně B5.
Pozvánka
Každoročně organizujeme přípravné opakovací kurzy zejm. matematiky před nástupem do bakalářského studia prvního ročníku pro studenty vybraných fakult a studijních programů TUL. Níže naleznete u názvu své fakulty případně porgramu pozvánka v PDF s detailními informacemi a odkaz na přihlašovací formulář.
Fakulta strojní
- ✉️ Pozvánka: zvaci_dopis_2024_FS.pdf
- 📋 Přihlašovací formulář: https://forms.gle/AGQYJmExTg9q8gUz8
Fakulta mechatroniky, informatiky a mezioborových studií
- ✉️ Pozvánka: zvaci_dopis_2024_FM.pdf
- 📋 Přihlašovací formulář: https://forms.gle/pZALVtSyrPd9jbcC7
Fakulta zdravotnických studií
- ✉️ Pozvánka: zvaci_dopis_2024_FZS.pdf
- 📋 Přihlašovací formulář: https://forms.gle/VGdMnThjRCyUaeRE7
Fakulta přírodovědně-humanitní a pedagogická
program Matematika se zaměřením na vzdělávání
- ✉️ Pozvánka: zvaci_dopis_2024_FP.pdf
- 📋 Přihlašovací formulář: https://forms.gle/qzmaYCZsAitautHc8